Introduction
I guess it was around 2005 or 2006 when I came across Quantum Computing from a college senior’s presentation in their final year. All I remembered from that was a Qubit being able to store twice the amount of data compared to a classical bit (either 1 or 0).
The correct explanation however is:
A single qubit can theoretically hold an infinite number of values in a superposition, but when measured, it can only yield one of two possible outcomes (0 or 1). The real power of qubits lies in their ability to exist in superposition and entangle with other qubits, enabling complex quantum computations that classical bits cannot achieve.
Althought it was mentioned to be a revolutionary idea that would change the world back then, nothing major happened to make it into public news until Google built a Quantum Computer.
Even so, I had to work hard to make sense of Quantum Mechanics as none of these concepts can be related to our real (classical) world. After making some progress into the theoretical side of things, I questioned why not delve into Quantum Computing and see how it is shaping up and solving problems quicker. There is also the threat of Quantum Computers being able to easily break many encryption systems that rely on time and memory constraints of classical computers.
Beginning the journey
I enrolled in University of Chicago’s ‘Quantum Computing for Everyone’ course in Dec 2023. Although I was able to complete the course, I would have absorbed maybe 25% of what was covered. The first couple of chapters were easier to follow, but the last few were kind of complex. It would have been nice to rewatch the course couple of times to better understand, but sadly it got completed and was inaccessible afterwards.
Things got a little out of hand when I borrowed Quantum Mechanics Demystified from the library to learn more about Quantum Mechanics at my own pace, but I quickly realized it was beyond me as it is Math Heavy and to be used as a referece book if you are trying to pass a Doctorate exam. I couldn’t even read some of the formulas leave alone understand any problems which were common on each page.
Getting hands-on
Motivated by the UC course, I decided to get my hands into some Q# and Quantum Simulator using Microsoft Quantum SDK. The current version of the SDK is very easy to install and use. The most important aspect of the Quantum Simulator is the use or simulation of various Quantum Gates, which are similar to the gates used in classical computation (AND, OR, XOR, NOT etc.). We need to make use of these Quantum Gates for almost all Quantum operations and algorithms.
Superposition
Let’s take a look at a basic Q# program that explores the concept of Superposition. Remember the thought experiment about Schrödinger’s cat. Instead of imaginary cats, we will use a Qubit.
Here we allocate a single Qubit, put it into superposition using the H Gate.
If we inspect the state of the system, we can see that the qubit has an equal (50%) probability to be in |0> and |1> basis states which indicates the single qubit is in a combination of both 1 and 0.
Interstingly the amplitude of both states is 0.7071 or 1/√2, since the sum of the squares of the amplitudes must be equal to 1.
Basis | Amplitude | Probability | Phase
-----------------------------------------------
|0⟩ | 0.7071+0.0000𝑖 | 50.0000% | 0.0000
|1⟩ | 0.7071+0.0000𝑖 | 50.0000% | 0.0000
When we measure it’s value, the superposition collapses and the result would be one of the basis states |0> or |1>.
namespace Quantum.Concepts {
open Microsoft.Quantum.Convert;
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Canon;
@EntryPoint()
operation Superposition() : Result {
// Qubits are only accesible for the duration of the scope where they are allocated
use qubit = Qubit();
// Set the qubit in superposition by applying a Hadamard transformation.
H(qubit);
// Measure the qubit. There is a 50% probability of measuring either `Zero` or `One`.
let result = M(qubit);
// Reset the qubit so it can be safely released.
Reset(qubit);
// Result would be either Zero or One
return result;
}
}
Source: Superposition.qs
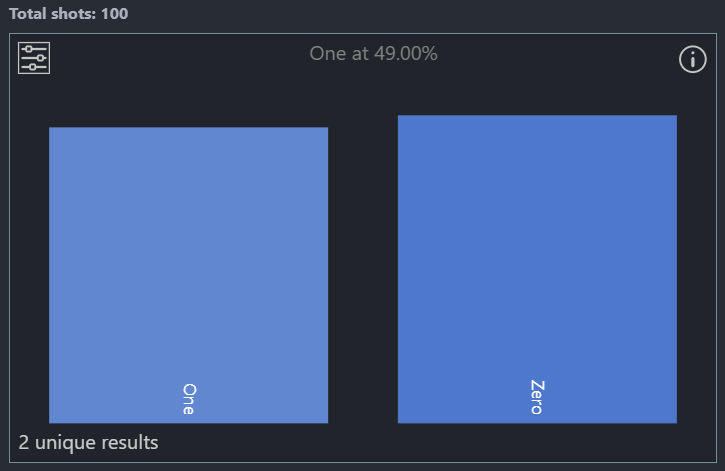
Upon running this operation 100 times, we see a close to even distribution of results. Every time we repeat the experiment the values would change, but the distribution is close to 50%, same if we do a Coin flip many times in the real world.
Entanglement
Entanglement is one of the most common quantum phenomena that we hear about. But it is difficut to understand as we do not observe this in our classical world.
Imagine two people, Alice and Bob, with boxes that contain balls. Each ball can be red or blue. According to classical physics, if Alice and Bob each open their box, the color they find should depend only on the contents of their respective boxes. However, quantum mechanics suggests that if the boxes are entangled, the color one person sees when opening their box can instantaneously determine the color seen by the other person, no matter how far apart they are.
namespace Quantum.Concepts {
open Microsoft.Quantum.Diagnostics;
@EntryPoint()
operation EntangleQubits() : (Result, Result) {
// Allocate the two qubits that will be entangled.
use (qAlice, qBob) = (Qubit(), Qubit());
// Set the first qubit in superposition by calling the `H` operation,
// which applies a Hadamard transformation to the qubit.
// Then, entangle the two qubits using the `CNOT` operation.
H(qAlice);
// Also known as the controlled-X gate, it flips the target qubit if the control
// qubit is in the ∣1⟩ state. It is an entanglement generator.
CNOT(qAlice, qBob);
// Measurements of entangled qubits are always correlated.
let (m1, m2) = (M(qAlice), M(qBob));
Reset(qAlice);
Reset(qBob);
return (m1, m2);
}
}
Source: Entanglement.qs
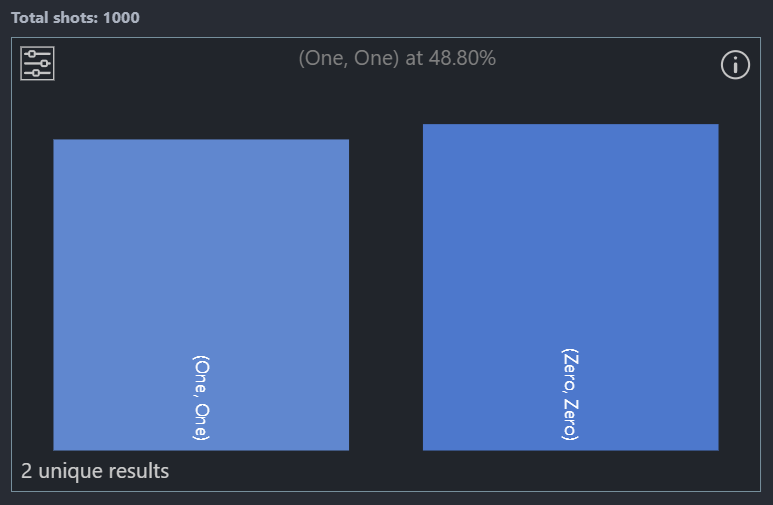
Here when the operation is executed 1000 times, we can see the results are around 50%, but the values of both the qubits are always in sync as they are entangled until measured.
Teleportation
Quantum teleportation is the phenomenon which is most interesting to me. It is related to the 2022 Nobel Prize in Physics, which proved Bell Inequality. This even baffled the great Einstein and led to EPR Paradox, both of which are beyond the scope of this blog post.
Quantum teleportation is a phenomenon in quantum mechanics where the quantum state of a particle is transmitted from one location to another, without the particle itself physically traveling through the intervening space. This process relies on the principles of quantum entanglement and classical communication.
operation Teleportation(sentMessage: Bool) : Bool {
mutable messageReceived = false;
// An array of three qubits allocated, representing the message qubit, Alice's qubit, and Bob's qubit.
use register = Qubit[3];
let message = register[0];
// The first qubit is set to the state |1⟩ if sentMessage is true, otherwise it remains in the state |0⟩.
if(sentMessage) {
// Flip the qubit to |1> state
X(message)
}
let alice = register[1];
let bob = register[2];
// An entangled pair is created where the two qubits become correlated such that
// their states are entangled. Any changes made to one qubit will instantaneously
// affect the other qubit, regardless of the distance between them.
H(alice);
// CNOT gate is applied with alice as the control and bob as the target, creating an entangled state between them.
CNOT(alice, bob);
// We want to teleport the message Qubit to Bob by entangling it with alice
// The message qubit is entangled with Alice's qubit using a CNOT gate.
CNOT(message, alice);
H(message);
// To teleport the qubit, Alice performs a special quantum measurement known
// as a Bell measurement on her qubit and the entangled qubit. This measurement
// is a joint measurement that extracts two classical bits of information.
let messageState = M(message);
let aliceState = M(alice);
// Based on the outcome of the Bell measurement, Alice obtains two classical
// bits of information that she sends to Bob through classical communication channels.
// These bits contain information about the measurement result.
// Upon receiving the two classical bits from Alice, Bob uses this information to
// perform a series of quantum operations on his qubit.
// The classical bits received by Bob from Alice determine which of the four possible quantum
// operations Bob should apply to his qubit. These operations are:
// 00 Outcome: If Alice's measurement result yields 00, Bob's qubit is already in the correct state, so no further action is needed.
// 01 Outcome: If Alice's measurement result yields 01, Bob applies a Pauli-X gate (bit-flip gate) to his qubit.
// This gate flips the state of Bob's qubit, effectively changing |0⟩ to |1⟩ and |1⟩ to |0⟩.
// 10 Outcome: If Alice's measurement result yields 10, Bob applies a Pauli-Z gate (phase-flip gate) to his qubit.
// This gate introduces a phase flip, leaving the basis states unchanged but introducing a phase of -1 to the |1⟩ state.
// 11 Outcome: If Alice's measurement result yields 11, Bob applies both a Pauli-X gate (bit-flip gate) and a Pauli-Z gate (phase-flip gate) to his qubit.
// This combination of gates effectively performs both a bit-flip and a phase-flip operation.
// Apply Pauli-Z gate (phase-flip gate) to Bob's Quibt
if messageState == One {
Z(bob);
}
// Apply Pauli-X gate (bit-flip gate) to Bob's qubit.
if aliceState == One {
X(bob)
}
// After Bob applies the appropriate quantum operation, his qubit is now in
// the exact same state as the original qubit that Alice wanted to teleport.
let bobState = M(bob);
if bobState == One {
set messageReceived = true;
}
// While the quantum state information is communicated instantaneously through
// the entangled qubits, the classical information obtained from the measurement
// result and the subsequent quantum operation by Bob are communicated classically,
// which is subject to the limitations of classical communication speed.
// As a result, the overall teleportation process does not occur instantaneously;
// it is limited by the speed of classical communication.
// Reset all the qubits that we used
ResetAll(register);
return messageReceived;
}
Source: Teleportation.qs
Alice wants to teleport the quantum state of her particle to Bob, who is far away. They share a pair of entangled particles, and Alice performs a Bell-state measurement on her particle and her part of the entangled pair, sending the result to Bob. With this classical information, Bob can manipulate his part of the entangled pair to recreate the state of Alice’s original particle. This process effectively teleports the state from Alice to Bob.
Quantum Algorithms
At an application level, Quantum Computing is aimed at certain types of problems which Classical computers cannot solve or take an absurd amount of time to solve. This includes Shor’s Algorithm which can find factors of a Prime Number faster than classical computers.
While current physical Quantum Computers have only demonstated it working upto small numbers due to need for more Qubits, quantum decoherence and error correction, it could one day easily break cryptography and encryption that we use in our daily digital lives. Hence a lot of governments and private companies are researching to gain an upper hand in this field.
References